In collaborazione con D. Perrone. Le metriche di Berger, ben note in Geometria Riemanniana, sono definite come la variazione canonica gλ, λ>0, della metrica standard g0 di curvatura sezionale costante di S3, ottenuta deformando g0 lungo le fibre della fibrazione di Hopf.
Siano {ξ1, ξ2, ξ3} i campi di vettori unitari su S3 che corrispondono alle strutture complesse standard I, J, K. Indicate con θ1, θ2, θ3 le 1-forme duali a ξ1, ξ2, ξ3 rispetto a g0, una arbitraria metrica di Berger gλ su S3 si scrive come gλ=λθ1⊗θ1+θ2⊗θ2+θ3⊗θ3. È allora naturale generalizzare tale costruzione, permettendo deformazioni di g0 non solo nella direzione di ξ1, ma anche di ξ2 e ξ3. Consideriamo quindi su S3 la famiglia a tre parametri di metriche Riemanniane della forma ḡλμν=λθ1⊗θ1+μθ2⊗θ2+νθ3⊗θ3, λ, μ, ν > 0.
Ovviamente, le metriche di Berger sono di questo tipo, essendo gλ=ḡλ11.
Le metriche ḡλμν si situano al crocevia di diversi interessanti temi di Geometria Riemanniana: campi di Hopf, applicazione di Hopf, metriche invarianti su SU(2), metriche di Berger, spazi omogenei e strutture omogenee, metriche naturali sul fibrato sferico tangente, morfismi armonici, strutture di quasi contatto e di contatto.
Anzitutto, esse risultano correlate ad una ben nota classe di metriche Riemanniane g-naturali definite sul fibrato sferico tangente T1S2(κ). Per tale motivo, tali metriche sono state chiamate "tipo Kaluza-Klein". La loro corrispondenza con le metriche Riemanniane g-naturali su T1S2(κ) consente di provare che una sottoclasse a due parametri di tali metriche determina dei corrispondenti morfismi armonici da S3 in S2 [1,2], che includono l'applicazione di Hopf tra le sfere standard come caso speciale.
D'altro canto, tali metriche possono essere interpretate come metriche Riemanniane invarianti a sinistra su SU(2). Quindi, (S3,ḡλμν) è uno spazio omogeneo. La classificazione delle strutture omogenee su (S3,ḡλμν) (vedi anche [3]) mostra come tali strutture dipendano dal numero distinto di parametri tra λ, μ e ν.
Si è anche introdotta una struttura naturale di quasi contatto su una arbitraria sfera (S3,ḡλμν), la quale fornisce esempi di spazi omogenei di quasi contatto. Numerose proprietà metriche di quasi contatto e di contatto di tali sfere sono state studiate.
[1] G. Calvaruso e D. Perrone, Harmonic morphisms and Riemannian geometry of tangent bundles, Ann. Glob. Anal. Geom., 39 (2010), 187-213.
[2] G. Calvaruso e D. Perrone, Harmonic morphisms and Kaluza-Klein metrics on the sphere S3, submitted.
[3] P.M. Gadea and J.A. Oubiña, Homogeneous Riemannian structures on Berger 3-spheres, Proc. Edinburgh Math. Soc.,
Parlerò di 4-varietà reali e lisce la cui olonomia di Chern ha dimensione 0 oppure 1. Usando qualche esempio significativo di natura simplettica vorrei spiegare come P.-A. Nagy (Greifswald, D) ed io arriviamo ad una classificazione.
[1] P.-A.Nagy e S.Chiossi, Systems of symplectic forms on four-manifolds, arXiv:1102.1995.
[2] P.-A.Nagy e S.Chiossi, Complex homothetic foliations on Kähler manifolds, Bull. London Math. Soc., in stampa.
La quantizzazione geometrica per varietà di Poisson che abbiano una foliazione simplettica singolare passa attraverso la costruzione del gruppoide simplettico integrante. A partire dalla descrizione esplicita di questo gruppoide per una naturale struttura di Poisson SU(2)-covariante sulla sfera S2, mostreremo quali altri problemi debbano essere superati per portare a termine la costruzione. In particolare descriveremo il ruolo svolto nella quantizzazione dalla classe modulare.
Il flusso di evoluzione nel senso di Hitchin permette di costruire metriche esplicite di coomogeneità uno con olonomia SU(3). Si parte cioè da un'orbita principale G/H con una struttura hypo e si risolve un'opportuna ODE, ottenendo una metrica sul prodotto G/H×(a,b) con olonomia contenuta in SU(3). In questo seminario illustrerò la classificazione delle metriche di questo tipo in cui il gruppo che agisce è nilpotente di dimensione 5. Questa classificazione comporta in particolare la risoluzione di un certo numero di ODE. Per ridurre il numero dei parametri, interpretando il flusso in termini di trasformazioni di gauge e usando il fatto che lo stabilizzatore principale è discreto, ci si riconduce a studiare un flusso sulla varietà delle algebre di Lie nilpotenti.
Spiegherò infine come non sia possibile estendere queste metriche a metriche complete di coomogeneità uno.
In the present talk I will introduce the notion of a generalized pseudohermitian structure on an almost CR manifold (M,HM,J). It is defined as a pair (h,P), where h is a positive definite fiber metric on HM compatible with J, and P:TM→TM is a smooth projector such that Im(P)=HM [1]. Generalized pseudohermitian structures are classified into sixteen classes, making use of a basic differential operator invariant under equivalence, that we call the Koszul operator. To each generalized pseudohermitian structure one can associate a canonical linear connection on the holomorphic bundle HM which is invariant under equivalence. By using this connection, the equivalence problem is solved under the assumption that the distribution HM has kind 2. This is a generalization of a classical result of Webster for pseudohermitian manifolds [4], in which case the canonical connection is the Tanaka-Webster connection [3], [4]. The curvature of the canonical connection will also be described, especially for the classes of standard homogeneous CR manifolds and 3-Sasakian manifolds. The basic formulas for isopseudohermitian immersions will be presented in the attempt to enlarge the theory of pseudohermitian immersions between strongly pseudoconvex pseudohermitian manifolds of hypersurface type [2].
[1] G. Dileo and A. Lotta, Generalized pseudohermitian manifolds, Forum Math., DOI: 10.1515/FORM.2011.098.
[2] S. Dragomir, On pseudo-Hermitian immersions between strictly pseudoconvex CR manifolds, Amer. J. Math. 117 (1995), no. 1, 169-202.
[3] N. Tanaka, On non-degenerate real hypersurfaces, graded Lie algebras and Cartan connections, Japan. J. Math. 20 (1976), 131-190.
[4] S. M. Webster, Pseudo-Hermitian structures on a real hypersurface, J. Differential Geom. 13 (1978), no. 1, 25-41.
Presenterò un tipo di geometria Riemanniana speciale in dimensione nove, associata ad una particolare 4-forma differenziale, con l'idea di ottenere una generalizzazione della selfduality in dimensione maggiore di 4. In particolare verrano esaminate le analogie tra questa geometria in dimensione 9 e la geometria Riemanniana in dimensione 4. I risultati si basano su un lavoro in collaborazione con Pawel Nurowski.
Let (M,η) be a contact manifold of dimension N=2n+1, n>1. It is well known that there exists a unique globally defined vector field ξ, called the Reeb vector field, which is transverse to the contact distribution Ker(η), such that η(ξ)=1 and dη(X,ξ)=0 for every smooth vector field X on M. It was proved by D. E. Blair in [2] that no flat associated metric can exist on (M,η), provided N>5. On the contrary, three-dimensional flat contact metric manifolds do exist (see [1]). We recall that an associated metric g is a Riemannian metric for which there exists a (1,1) tensor field ϕ such that ϕ2=-Id+η⊗ξ, η(X)=g(X,ξ), dη(X,Y)=g(X,ϕY) for every X,Y vector fields on M. Then ϕ restricts to a partial complex structure J on the contact distribution; when J is integrable, (M,J,η) is a pseudohermitian manifold.
More generally, Z. Olszak showed that if N>5 and one asks for constant sectional curvature c, then c must be equal to 1, and the structure must be Sasakian, i.e. J is integrable and ξ is Killing [5]. It is also relevant that a compact contact manifold cannot admit any associated metric of negative curvature; this is settled by a result of A. Zeghib on geodesic plane fields, because for every associated metric the integral curves of ξ are geodesics (cf. [1, Theorem 7.4]).
In the light of these facts, Blair conjectured the non existence of contact metric manifolds having nonpositive curvature, with the exception of the flat 3-dimensional case. We shall discuss a recent result which confirms this conjecture for homogeneous contact manifolds [4]:
Theorem
Let (M,ϕ,ξ,η,g) be a homogeneous simply connected contact metric manifold having nonpositive sectional curvature. Then M is 3-dimensional, flat, and it is equivalent to the Lie group Ē(2), universal covering of the group of Euclidean motions of ℝ2, endowed with a left invariant contact metric structure.
Actually, a more general result has been obtained in [4]; let us call a Riemannian metric g on (M,η) admissible if the Reeb vector field ξ is of unit length and orthogonal to the contact distribution with respect to g. Of course, every associated metric is admissible.
Theorem
Let (M,η) be a homogeneous simply connected contact manifold of dimension N≥5. Then M does not admit any admissible homogeneous Riemannian metric g having nonpositive curvature.
This fact suggests to perform a deeper study of the class of admissible metrics for contact forms. We shall present some work in progress in this direction, in particular concerning the case of Levi-parallel contact Riemannian manifolds [3]. They constitute a nice class including pseudohermitian and Sasakian manifolds in a natural fashion. The integrability condition for the partial complex structure is substituted by the parallelism of the Levi form of the contact distribution with respect to a canonical metric connection parallelizing η, which plays the role of the Tanaka-Webster connection in pseudohermitian geometry [6],[7].
[1] D. E. Blair, Riemannian geometry of contact and symplectic manifolds, Progr. Math. 203, Birkhäuser, Boston, 2002.
[2] D. E. Blair, On the non-existence of flat contact metric structures, Tohoku Math. J. (2) 28 (1976), 373-379.
[3] G. Dileo and A. Lotta, Levi-parallel contact Riemannian manifolds, (2011), in preparation.
[4] A. Lotta, Non existence of homogeneous contact metric manifolds of nonpositive curvature, Tohoku Math. J. 62 (2010), 575-578.
[5] Z. Olszak, On contact metric manifolds, Tohoku Math. J. (2) 31 (1979), 247-253.
[6] N. Tanaka, On non-degenerate real hypersurfaces, graded Lie algebras and Cartan connections, Japan. J. Math. 20 (1976), 131-190.
[7] S.M. Webster, Pseudo-Hermitian structures on a real hypersurface, J. Differential Geom. 13 (1978), no. 1, 25-41.
We study reducible SO(3)-structures of special type on 8-dimensional Riemannian manifolds. These determine altogether a triple family of G-structures: an almost-product, a PSU(3) and an almost quaternion-Hermitian structures. The relations between these G-structures are investigated showing that any two of them determine the third. It is shown that in the case of invariant intrinsic torsion the SO(3)-geometry is controlled by a subcomplex of the de Rham complex. As an example of the classification a Nearly Quaternionic structure is found on SU(3).
Presentiamo alcuni recenti risultati di una collaborazione con Stere Ianus, Liviu Ornea e Radu Pantilie. In un ambito generale e non metrico si è introdotta la classe delle varietà CR quaternionali, delle quali fanno parte le varietà quaternionali e che in dimensione 3 si riducono essenzialmente a varietà conformi, nonché la rispettiva nozione di applicazioni CR quaternionali. Abbiamo anche mostrato che per tali varietà e applicazioni è possibile sviluppare una ricca e naturale teoria twistoriale. Inoltre si è stabilito che, sotto ipotesi piuttosto generali, una varietà CR quaternionale può ottenersi come sottovarietà di una varietà quaternionale. Si accennerà a qualche applicazione alle sottovarietà di una varietà quaternionale.
[1] S. Ianus, S. Marchiafava, L. Ornea, R. Pantilie, Twistorial maps between quaternionic manifolds, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5), Vol. IX (2010), 47-67.
[2] S. Marchiafava, L. Ornea, R. Pantilie, Twistor theory for CR quaternionic manifolds and related structures, Monatsch. Math., Online First, 24 June 2011.
[3] S. Marchiafava, R. Pantilie, A note on CR quaternionic maps, arXiv:1108.3199v1 [math.DG] 16 Aug 2011, submitted.
Discuteremo alcuni risultati classici ed alcuni recenti sull'immagine della mappa di Gauss delle superfici minime complete, specialmente nel caso di quelle di curvatura totale finita. Per queste ultime è ancora aperto il problema di determinare l'esistenza o meno di una tale superficie la cui mappa di Gauss omette tre punti.
The talk aims to introduce the general problem of determining Intrinsic Torsion Varieties (ITV's) of reduced Riemannian structures over a parallelizable manifold. A geometrically relevant classification of G-structures is based on criteria whereby the intrinsic torsion tensor of the structure belongs to a proper subset of G-irreducible components of the corresponding space of intrinsic torsion. The set of reductions of the same type of a G-structure over a parallelizable manifold is described in terms of a standard parameter space. The ITV's of reductions of a given type are the submanifolds of the parameter space whose points correspond to structures of the same null-torsion class. From this point of view Riemannian almost-product structures present a rich phenomenology, which highlights some basic aspects of the theory. We provide a complete description of the ITV's of SO(3)×SO(3) and SO(2)×SO(4) reductions of a standard invariant Riemannian structure on the Iwasawa manifold. In the case of SO(2)×SO(4), the almost product structures are parametrized by the Grassmannian of two-planes in ℝN, which is a coadjoint orbit of SO(6). The canonical symplectic structure on this space (with the corresponding moment map) is strongly involved in the description of the ITV's.
Le sottovarietà minime (armoniche) di una varietà riemanniana N sono quelle il cui vettore curvatura media H è identicamente nullo. Una generalizzazione naturale delle sottovarietà minime è costituita dalle sottovarietà biarmoniche le quali sono caratterizzate dalla condizione ΔH+Trace R(⋅,H)⋅=0, dove Δ rappresenta il laplaciano grezzo mentre R indica l'operatore di curvatura della varietà N. Nel caso delle ipersuperfici, la condizione di biarmonicità coincide con la richiesta che la funzione curvatura media H e l'operatore di forma A soddisfino al sistema
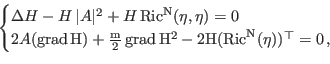
dove η è un campo di vettori normale unitario, mentre Ric indica l'operatore di Ricci di N.
Le sottovarietà biarmoniche sono state oggetto di intensi studi negli ultimi dieci anni ed ancora rimane irrisolta la congettura di B.-Y. Chen: le uniche sottovarietà biarmoniche di ℝ sono le minime.
In questa comunicazione mostreremo alcuni risultati recenti sulla classificazione delle sottovarietà biarmoniche nelle forme spaziali.
The dynamics of shapes in many physical and biological systems can be described in terms of local motions of curves and surfaces. Of particular interest are local motions whose dynamics is described by completely integrable evolution equations. Paradigmatic examples are the Goldstein-Petrich motions of curves in the Euclidean plane. Local motions of curves in two-dimensional Klein geometries, (affine, centro-affine conformal and projective) have been studied, among others by Calini, Chu and Qu, Doliwa and Santini, Ivey, Langer, Mari-Beffa, Perline, Pinkall. In this talk I will focus on local motions of curves in projective plane, and I will explain how to construct a sequence of local dynamics of curves in ℝℙ2 inducing the Kaup-Kupershmidt hierarchy of integrable evolution equations.
In collaborazione con Paolo Piccinni e Victor Vuletescu. Si indicherà una semplice costruzione algebrica della 8-forma Phi caratterizzante le strutture Spin(9) su varietà 16-dimensionali. Inoltre, si mostrerà come Spin(9) è responsabile dell'esistenza di più di 7 campi tangenti sulle sfere Sn-1 (cosa che può accadere soltanto quando n è divisibile per 16).
Joint work with Paolo Piccinni and Victor Vuletescu. I will show a simple construction of the 8-form Phi characterizing Spin(9) structures on 16-dimensional manifolds. Moreover, I will show how the existence of more than 7 independent tangent vector fields on spheres is all the fault of Spin(9).
La nozione di spazio Γ-simmetrico introdotta da R. Lutz in [2] è una generalizzazione della nozione classica di spazio simmetrico. Sia Γ un gruppo abeliano finito e sia G un gruppo di Lie connesso.
Definizione
Uno spazio Γ-simmetrico è uno spazio omogeneo riduttivo M=G/K munito in ogni punto di un gruppo abeliano finito di simmetrie isomorfo a Γ.
Ossia esiste un omomorfismo iniettivo ρ:Γ→Aut G, tale che GΓ0⊆ K ⊆ GΓ, dove GΓ è il sottogruppo di elementi fissati da ρ(Γ) e GΓ0 è la sua componente connessa.
Il caso Γ=ℤ2 coincide con la definizione di spazio simmetrico, mentre se Γ=ℤ2k l'algebra di Lie di G è graduata da Γ e la graduazione permette di costruire le simmetrie di M. Nel caso Γ=ℤ22 possiamo riscrivere la definizione come segue.
Definizione
Uno spazio omogeneo M=G/K è Γ=ℤ22-simmetrico se e solo se esistono due diverse involuzioni che commutano in G, cioè se esistono σ,τ∈Aut G-{Id} (σ2=τ2=Id, σ≠τ e στ=τσ) tali che (Gσ∩Gτ)0⊆K⊆Gσ∩Gτ.
Una metrica riemanniana adattata a uno spazio Γ-simmetrico M è data da un tensore metrico per il quale le simmetrie sono isometrie (si veda [1]). Dopo aver descritto la classificazione, a meno di automorfismi dell'algebra di Lie, degli spazi ℤ22-simmetrici nel caso in cui M è il gruppo di Heisenberg viene descritto il tensore metrico riemanniano e quello pseudo-riemanniano adattato a queste strutture.
[1] M. Goze e E. Remm, Riemannian Γ-symmetric spaces, Differential geometry, World Sci. Publ., Hackensack, NJ, (2009), 195-206.
[2] R. Lutz, Sur la géométrie des espaces Γ-symétriques C.R.A.S. Paris S\'er. I Math. 293 (1981), no. 1, 55-58.
Illustro un lavoro in collaborazione con A. Spiro, in cui si studiano varietà nearly Kähler di dimensione sei con un gruppo compatto G di automorfismi che agisce con coomogeneità uno. Si classificano tali varietà nel caso compatto a meno di G-diffeomorfismi; si costruisce poi una nuova famiglia ad un parametro di metriche nearly Kähler sul tangente della sfera S3, contenente esattamente due metriche localmente omogenee.
Discuteremo le conseguenze spettrali della seguente situazione: M è una varietà Riemanniana compatta dotata di un'involuzione isometrica γ, tale che la distanza di un qualunque punto x∈M dalla sua immagine γ(x) sia limitata dal basso da una costante positiva β.
Ecco un caso particolare: M è immersa in una sfera, ed è invariante per l'azione antipodale. Si ottiene la stima universale λ2(D)-λ1(D)≤dim M, dove D è un qualunque operatore di tipo Laplace invariante per l'azione di γ e λ1, λ2 sono i primi due autovalori di D. L'uguaglianza implica che M è minima. Inoltre, se D è l'operatore di Hodge-Laplace agente sulle forme di grado p, l'uguaglianza vale se e solo se M è il toro di Clifford con p-esimo numero di Betti uguale a 1.
Le teorie di super-gravità sono generalizzazioni della Relatività Generale, in cui lo spazio-tempo è rappresentato da una varietà n-dimensionale M e la gravità è considerata parte di una collezione più complessa di campi fisici (la super-gravità, per l'appunto). Nel seminario si fornirà una presentazione di tali campi e delle loro equazioni in termini di campi tensoriali di una (super)varietà M', in cui lo spazio-tempo M è immerso. Per i suoi contenuti, il seminario è destinato ad un pubblico matematico e non richiede particolari conoscenze di Fisica. È finalizzato a mostrare come questioni in supergravità sono riconducibili a studi su enti geometrici, che sono naturali generalizzazioni delle varietà di Einstein e delle varietà CR.
In this talk I will discuss recent results on the geometry of constant mean curvature (H not 0) surfaces embedded in ℝ3. Among other things I will prove radius and curvature estimates for simply connected surfaces embedded in ℝ3 with constant mean curvature. It follows from the radius estimate that the only complete, simply connected surface embedded in ℝ3 with constant mean curvature is the round sphere. This is joint work with Bill Meeks.
Lo scopo di questa comunicazione è quello di illustrare alcune tecniche per costruire strutture complesse e quasi complesse che non siano compatibili con forme simplettiche. Parte del seminario sarà dedicato a strutture quasi complesse non dominabili da forme simplettiche; questo argomento è collegato al flusso Hermitiano introdotto da Streets e Tian e con una recente congettura di Donaldson in dimensione 4.