A property very important in social networks, and to a lesser degree in other networks, is transitivity. If refers to the extent to which the relation that relates two nodes in a network that are connected by an edge is transitive. Perfect transitivity implies that, if $x$ is connected (through an edge) to $y$, and $y$ is connected to $z$, then $x$ is connected to $z$ as well. It is very rare in real networks, since it implies that each component is a clique, that is, each pair of reachable nodes in the graph would be connected by an edge.
However, partial transitivity is useful. In many networks, particularly social ones, the fact that $x$ knows $y$ and $y$ knows $z$ does not guarantee that $x$ knows $z$ as well, but makes it much more likely. The friend of my friend is not necessarily my friend, but is far more likely to be my friend than some randomly chosen member of the population.
We can quantify transitivity in an undirected network as follows. A loop of length three is a sequence of nodes $x, y, z, x$ such that $(x,y)$, $(y,z)$ and $(z,x)$ are edges of the graph. Notice that this is the smallest loop possible in an undirected network. A path of length two is a sequence of nodes $x, y, z$ such that $(x,y)$ and $(y,z)$ are edges (the edge $(z,x)$ can be present or not). Notice that paths (and loops) are sequences, hence the loop $x, y, z, x$ is different from $y, z, x, y$. The transitivity coefficient $T$ of a network, also known as clustering coefficient, is the ratio of the number of loops of length three and the number of paths of length two. Hence, it is the frequency of loops of length three in the network.
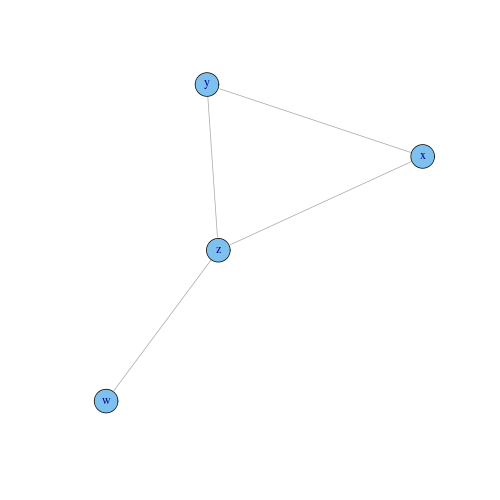
$T = 1$ implies perfect transitivity, i.e., a network whose components are all cliques. $T=0$ implied no closed path of length two, which happens for various topologies, such as a tree or a square lattice. For instance, in the next graph, we have 6 loops of length three (2 starting at $x$, 2 starting at $y$, and 2 starting at $z$) and 10 paths of length 2 (3 starting at $x$, 3 starting at $y$, 2 starting at $z$, and 2 starting at $w$), hence $T = 6/10 = 0.6$.
transitivity(g) [1] 0.6

In the context of social networks, three individuals $x, y, z$ such $x$ and $z$ are both friends of $y$ are called a triad centered at $y$. The triad is said open if the link from $x$ to $z$ is missing. A closed triad centered at $y$ is a particular triad centered at $y$ with the additional link from $x$ to $z$. The process of closing an open triad is called triadic closure. In this context, the transitivity coefficient corresponds to the fraction of triads that are closed, that is the fraction of pairs of people with a common friend who are themselves friends, or equivalently, the mean probability that two people with a common friend are themselves friends. In the above example, for instance, there are 5 triads: one centered at $x$, one at $y$, and three at $z$. Three of them are closed triads (the ones on the triangle), and two are open (the ones centered at $z$ that include $w$). Hence the transitivity coefficient is $T = 3/5 = 0.6$, as computed above.
Social networks tend to have quite high values of the transitivity coefficient. For instance, the transitivity coefficient of the computer science collaboration network is 0.24. This means that, on average, the chance that two scholars that share a common collaborator wrote a paper together is almost one-fourth. This is a rather high probability, indeed. As a comparison, the transitivity coefficient for a random network of the same size is $9.6 \cdot 10^{-6}$. The transitivity coefficient of a random graph with $n$ nodes and $m$ edges is simply the density of edges $m / m_{*}$, where $m_* = n (n-1) / 2$ is the maximum number of edges of a graph of $n$ nodes. Moreover, for a network with the same degree distribution of our collaboration network but otherwise random transitivity is $1.4 \cdot 10^{-4}$. The transitivity coefficient of a random graph with degree sequence $k$ is
$\displaystyle{\frac{1}{n} \frac{[\langle k^2 \rangle - \langle k \rangle]^2}{\langle k \rangle^3}}$where $\langle k \rangle = 1/n \sum_i k_i$ is the mean degree and $\langle k^2 \rangle = 1/n \sum_i k_{i}^{2}$ is the mean square degree. Both values are orders of magnitude lower that what we computed on the real collaboration network. This large discrepancy is a clear sign of real social effect at work in the context of academic collaboration: authors with a common collaborator have several good reasons to write a paper together, for instance they are probably working on very close topics or they scientifically know each other through the common collaborator.
However, non-social networks have lower transitivity coefficients. For the Internet, for example, the transitivity is only 0.012, against an expected value, if connections were made at random, of 0.84. This suggests that in the Internet there are forces at work that shy away from the creation of triangles. In some other networks, such as food webs or the Web, transitivity is neither higher nor lower than expected.
An alternative definition for the transitivity coefficient, which is often referred to as clustering coefficient, of that of the mean local clustering coefficient of nodes in the network:
$\displaystyle{C = \frac{1}{n} \sum_{i} C_{i}}$Mind that this is a different definition from the transitivity coefficient $T$ defined above. This definition has the drawback that it tends to be dominated by vertices with low degree, since they have a small number of possible pairs of neighbors (the denominator of the local clustering coefficient). In particular, a node with only two neighbors which are connected each other has local clustering one. For this reason, the clustering coefficient $C$ is, in general, higher than the transitivity coefficient $T$. For the collaboration network in computer science, for instance, it is 0.75, where transitivity is 0.24. Moreover, for vertices of degree zero or one the local clustering coefficient is not defined (both numerator and denominator are 0). Hence for networks with a significant number of vertices with low degree, the clustering coefficient $C$ gives a rather poor picture of the overall properties of the network.
As for directed networks, the transitivity coefficient is computed as for undirected networks, but ignoring the direction of the edges. However, notice that, where on undirected graphs the smallest loop has length three, in a directed graph it has length two; it is a sequence $x,y,x$ such that the directed edges $(x,y)$ e $(y,x)$ belong to the graph. We can thus measure the frequency of loops of length two in a directed network, which is called reciprocity. It measures how likely it is that a vertex that you point to also points back at you. Formally, the reciprocity of a directed network is the fraction of edges that belong to a loop of length two, or:
$\displaystyle{R = \frac{1}{m} \sum_{i,j} A_{i,j} A_{j,i} = \frac{1}{m} \mathrm{Tr} \, A^2}$where $m$ the the number of edges and $A$ the adjacency matrix of the graph. Notice that $A_{i,j} A_{j,i} = 1$ if and only if $i$ links to $j$ and vice versa. For the Web, the reciprocity is about 57%, meaning that more than half of the links link back. For the network of who has whom in the email address book the reciprocity was found about 23%.
The transitivity measures the density of loops of length three (triangles) in a network. We can also look at densities of other small groups of nodes, or motifs, and they are called (the reciprocity in directed networks was an example, in fact). For instance, in genetic regulatory networks and neural networks researchers have found certain small motifs that occurred far more often than expected on the basis of chance. They conjectured that these motifs were playing the role of functional circuit elements, and that they might be an evolutionary result of their usefulness to the organisms involved.