
A shortest path, or geodesic path, between two nodes in a graph is a path with the minimum number of edges. If the graph is weighted, it is a path with the minimum sum of edge weights. The length of a geodesic path is called geodesic distance or shortest distance. Geodesic paths are not necessarily unique, but the geodesic distance is well-defined since all geodesic paths have the same length.
One large-scale property of networks is the average geodesic distance between pairs of nodes in the network. One of the most discussed network phenomena is the small-world effect. In most real network the typical geodesic distance is surprisingly short, in particular when compared with the number of nodes of the network.
The small-world effect has a substantial implication for networked systems. Suppose a rumor (or a disease) is spread over a social network. Clearly it will reach people much faster if it is only about six steps from any person to any other than if it is a hundred. Similarly, the speed with which one gets a response from another computer on the Internet depends on how many hops data packets have to make as they traverse the network.
In fact, once one looks deeply into the mathematics of networks, one discovers that the small-world effect is not so surprising after all. Mathematical models of networks suggest that path lengths in networks should typically scale as $\log n$ with the number $n$ of network nodes, and should therefore tend to remain small even for large networks. The rough idea behind this short distances is that the number of nodes one encounters in a breath-first visit of a graph starting from a source node typically increases exponentially with the distance to the source node, hence the distance increases logarithmically in the number of visited nodes.
One can also examine the diameter of the network, which is the largest geodesic distance in the graph. The diameter is usually found to be very small as well and calculations using network models suggest that it should scale logarithmically with the number of nodes as the average geodesic distance. The diameter is, however, a less useful measure for real networks than the average distance, since it really only measure the distance between one pair of vertices at the extreme end of the distribution of distances. Moreover, the diameter is sensible to small changes to the set of nodes, which makes it a poor indicator of the behavior of the network as a whole.
Let's check the average geodesic distance and the diameter for a random graph:
n = 100 p = 1.5/n g = erdos.renyi.game(n, p) # average geodesic distance average.path.length(g) [1] 5.773585 # diameter d = get.diameter(g) length(d) - 1 [1] 14 E(g)$color = "grey" E(g)$width = 1 E(g, path=d)$color = "red" E(g, path=d)$width = 2 V(g)$color = "SkyBlue2" V(g)[d]$color = "red" coords = layout.fruchterman.reingold(g) plot(g, layout=coords, vertex.label = NA, vertex.size=3)

For example, we computed the geodesic distances for all pairs of nodes in the computer science collaboration network. The next barplot shows the share of geodesics having a given length. Notice that geodesics have typically very short lengths compared to the number of nodes: 19% of geodesics have length 5, 33% have length 6, and 26% have length 7. The average geodesic distance is 6.41, and, interestingly, distances normally distribute around this peak. The largest distance is also remarkably small: 23 (there are 8 different geodesics with this length).
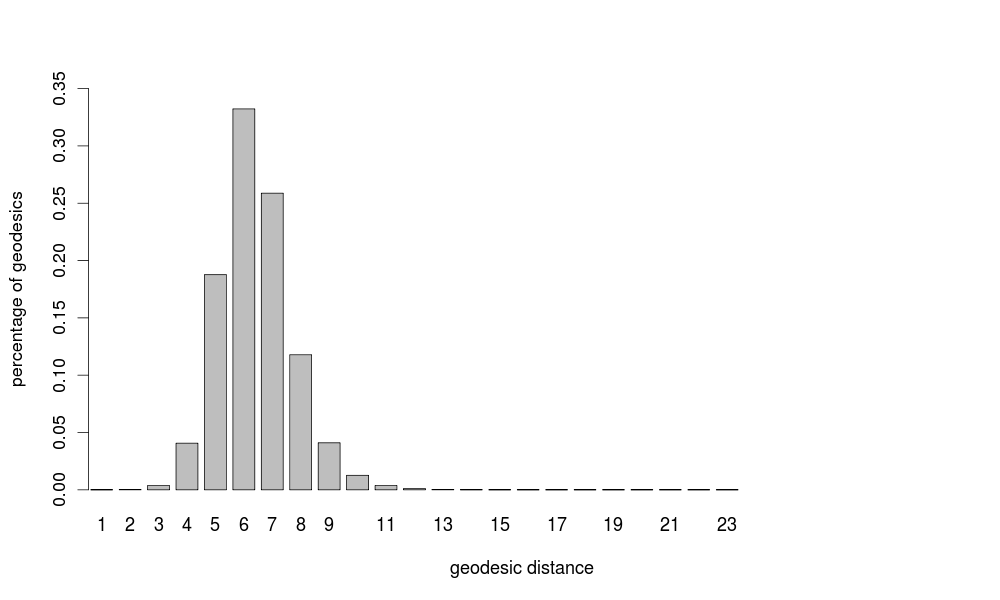
These are good news for the computing community: not only the collaboration network is mostly connected, but the average distance is short, and the longest one is not that longer. This means that scientific information can spread quickly on the great majority of the computing community through its collaboration network.
The fact that distances normally distribute is interesting because it means that the average distance of 6 links represents a typical value of all distances in the network. Furthermore, since the distribution of distances drops off rapidly around the mean, the time-consuming computation of the exact average distance can be approximated by computing the average distance on a relatively small random sample of node pairs.
It has been proposed to use paths on social networks as referral chains to establish contacts with domain experts. In the simplest case, suppose I am searching for a piece of information and I am aware that you are a domain expert that most likely can answer my query. If I do not know you personally, it might be useful to know that we have a common friend that can arrange an introduction. In general, we might use the intermediate people in referral chains in order to smoothly get in contact with the target person.
To be sure, the chance of success of the contact with the expert depends on the path length but also on the strength of the intermediate path links. If, for instance, I can reach the expert through either actor A or actor B, I know A much better than B, and the expert knows both A and B at the same way, common sense suggests to use A as a broker. Hence, we can imagine to weight the links of the social network with the inverse of the strength at which the connected actors know themselves, so that two actors are connected by a light edge if they know each other quite well. We can then look for light referral chains, that is, paths with a low summation of the weights of the edges. This opens an interesting question: is preferable a short and weighty path, or a longer and lighter one in order to reach a given domain expert? Notice that a short path has the obvious advantage of having few intermediate actors to bother, but a light path is desirable since the intermediate links are stronger and more reliable.
In the context of collaboration networks among scholars, for instance, one might reasonably argue that the intensity of the scientific relationship between two scholars is proportional to the number of papers they have written together. We can implement such an intuition by labeling each edge $(x,y)$ of the collaboration graph with a positive weight $1/k$, where $k$ is the number of papers that $x$ and $y$ have written together. The edge weight can be interpreted as a scientific distance among scholars: the more papers two authors have written together, the closer they are scientifically.
We have found that the average weighted distance on the computer science weighted collaboration network is 3.15, and the average length of the weighted geodesics is 11.27. Hence, light paths are much longer, almost twice longer, than the typical geodesic path, which is about 6 edges long. Furthermore, the average geodesic distance is 6.43, and the average weight of the geodesics is 5.07. Thus, short paths are significantly heavier than the typical weighted geodesic path, which weights about 3. Hence weighted shortest paths and unweighted shortest paths are different referral chains; the information seeker is hence faced with the dilemma of following short and weighty (unreliable) chains or long and light (reliable) paths in order to get in contact with the coveted expert.