Degree Centrality

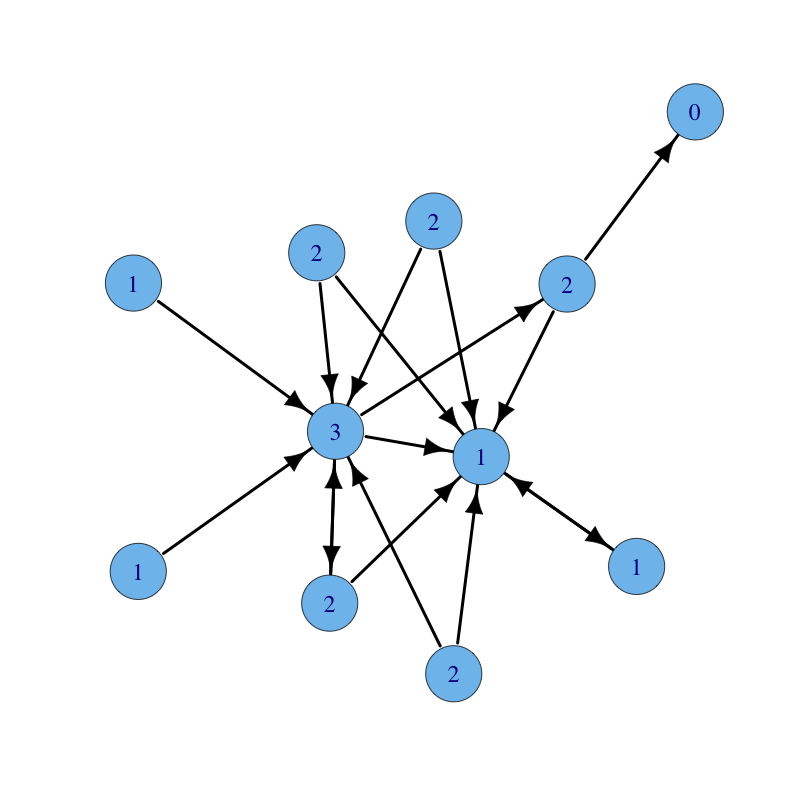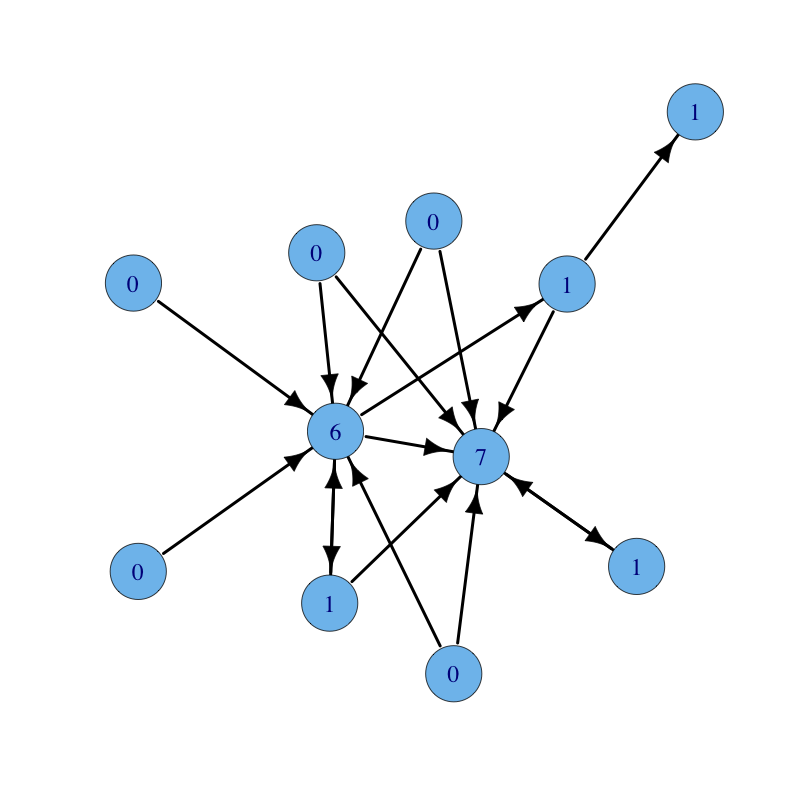
Degree is a simple centrality measure that counts how many neighbors a node has. If the network is directed, we have two versions of the measure: in-degree is the number of in-coming links, or the number of predecessor nodes; out-degree is the number of out-going links, or the number of successor nodes. Typically, we are interested in in-degree, since in-links are given by other nodes in the network, while out-links are determined by the node itself. Degree centrality thesis reads as follows:

A node is important if it has many neighbors, or, in the directed case, if there are many other nodes that link to it, or if it links to many other nodes.

Math

Let $A = (a_{i,j})$ be the adjacency matrix of a directed graph. The in-degree centrality $x_{i}$ of node $i$ is given by: $$x_{i} = \sum_k a_{k,i}$$ or in matrix form ($1$ is a vector with all components equal to unity): $$x = 1 A$$ The out-degree centrality $y_{i}$ of node $i$ is given by: $$y_{i} = \sum_k a_{i,k}$$ or in matrix form: $$y = A 1$$

Code

The built-in function degree (R, C) computes degree centrality.

A user-defined function degree.centrality follows:


# Degree centrality
# INPUT
# g = graph
# mode = degree mode ("in" for in-degree, "out" for out-degree, "all" for total degree)
degree.centrality = function(g, mode) {
  A = get.adjacency(g);
  o = rep(1, n);
  if (mode == "in") c = o %*% A else
    if (mode == "out") c = A %*% o else 
      c = o %*% (A + t(A)); 
  return(as.vector(c));
}

Example

A graph with nodes labelled with their in-degree centrality follows:

Next is the same graph with nodes labelled with their out-degree centrality: