A connected component of an undirected graph is a maximal set of nodes such that each pair of nodes is connected by a path. Connected components form a partition of the set of graph vertices, meaning that connected components are non-empty, they are pairwise disjoints, and the union of connected components forms the set of all vertices. Equivalently, we can say that the relation that associates two nodes if and only if they belong to the same connected component is an equivalence relation, that is it is reflexive, symmetric, and transitive.
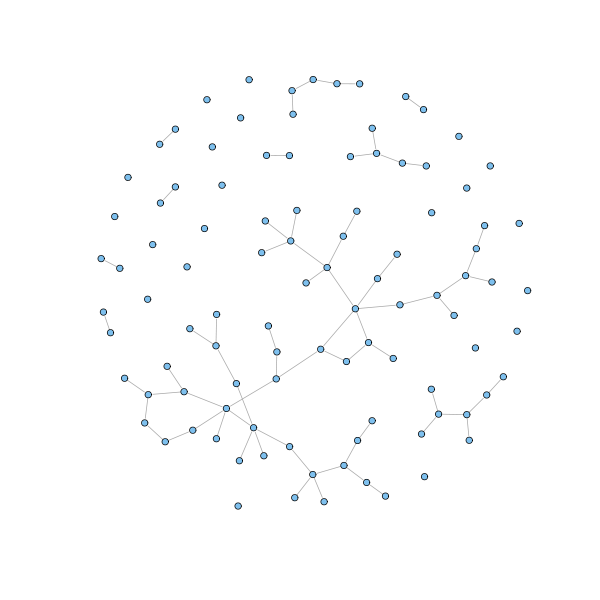
In real undirected networks, we typically find that there is a large component (the giant component) that fills most of the network - usually more than half and not infrequently over 90% - while the rest of the network is divided into a large number of small components disconnected from the rest. The situation is exemplified in the following figure.
n = 100 p = 1.5/n g = erdos.renyi.game(n, p) coords = layout.fruchterman.reingold(g) plot(g, layout=coords, vertex.size = 3, vertex.label=NA)

The network is drawn according to the the random model, also known as Erdős-Rényi model, the simplest and oldest network model. According to this model, a network is generated by laying down a number $n$ of nodes and adding edges between them with independent probability $p$ for each node pair.
You can plot an interactive version of the network and a 3D version of it as follows:
tkplot(g, layout=coords, vertex.label = NA, vertex.size=3) coords3D = layout.fruchterman.reingold(g, dim=3) rglplot(g, layout=coords3D, vertex.label = NA, vertex.size=3)
Commands that work with connected components are the following:
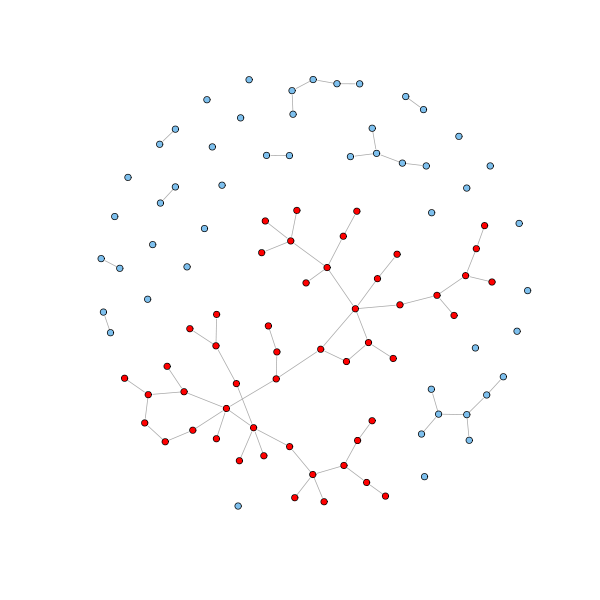
# Get the components of an undirected graph cl = clusters(g) # How many components? cl$no [1] 31 # How big are these (the first row is size, the second is the number of components of that size)? table(cl$csize) 1 2 5 7 50 21 6 2 1 1 # Get the giant component nodes = which(cl$membership == which.max(cl$csize)) # Color in red the nodes in the giant component and in sky blue the rest V(g)$color = "SkyBlue2" V(g)[nodes]$color = "red" plot(g, layout=coords, vertex.size = 3, vertex.label=NA)
There are some networks for which the largest component fills the entire network. In these cases there is always a good reason. The Internet is a good example. There would be no point in being part of the Internet if you are not part of its largest component, since that would mean that you are disconnected from and unable to communicate with almost everyone else. Other examples include power grids, train routes, and electronic circuits.
Can a network have two or more large components that fill a sizable fraction of the entire graph? Usually the answer is no. The argument is that if a network of $n$ nodes was divided into two large components of about $n/2$ nodes each, then there would be $n^2/4$ possible pairs of nodes such that one node was in one large component and the other node in the other large component. If there is an edge between any of these pairs, than the components are joined together into a single component. It is highly unlikely that not one such pair would be connected.
And what about networks with no large component? It is certainly possible. One example would be the network of immediate family ties. Networks like those, however, are not studied with the network analysis toolkit, since there is little to be gained by applying these techniques to such networks.
A useful generalization of the concept of connected component is the k-connected component (or simply k-component). A $k$-component is a maximal set of vertices such that each is reachable from each of the others by at least $k$ node-independent paths (paths that do not share any node unless the source and the target ones). For the common cases $k=2$ and $k=3$, $k$-components are called bicomponents and tricomponents.
A 1-component is just an ordinary component. Moreover, for $k \geq 2$, a $k$-component is nested within a $k-1$ component (every pair of nodes connected by $k$ independent paths is also connected by $k-1$ independent paths). Notice that for $k \geq 2$, $k$-components may overlap. Hence $k$-components do not define a partition of (or equivalence relation on) the set of vertices. An example is provided in the next graph.
g = graph(c(1,2, 1,3, 2,4, 4,3, 4,5, 4,6, 5,7, 7,6), directed=FALSE) coords = layout.fruchterman.reingold(g) plot(g, layout=coords)
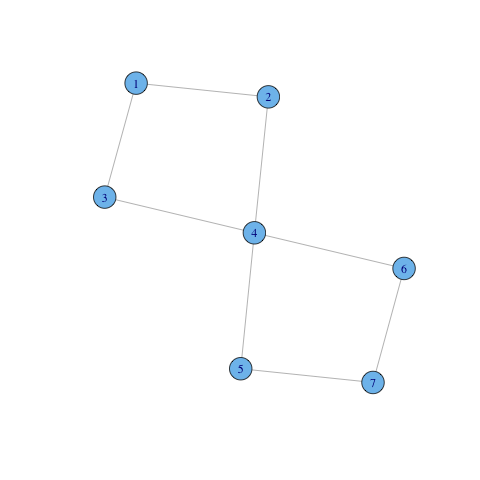
There are two bicomponents overlapping: $C_1 = \{1,2,3,4\}$ and $C_2 = \{4,5,6,7\}$. Vertex $3$ belongs to both components.
The command biconnected.components can be used to extract the biconnected components of a graph (it gives the components as a set of edge identifiers).
bc = biconnected.components(g) # print edge ids of biconnected components bc$component_edges # print edges of the first biconnected components E(g)[bc$component_edges[[1]]] # print node ids of biconnected components bc$components
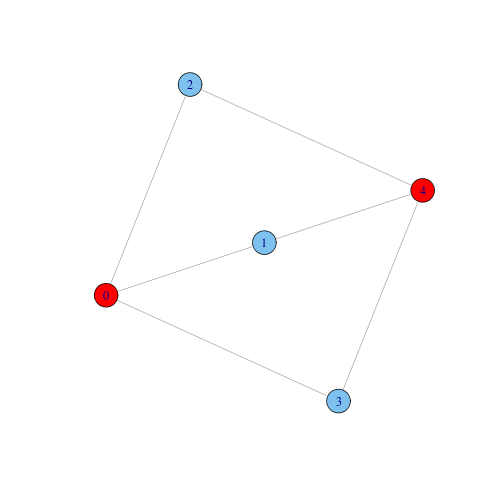
Note also that for $k \geq 3$, the $k$-components in a network can be non-contiguous. For instance, in the next graph, nodes 0 and 4 form a non-contiguous tricomponent. Notice that the tricomponent is embedded into a (contiguous) bicomponent that covers the whole graph. Within social networks literature, where non-contiguous components are often considered undesirable, $k$-components are defined in a different way to rule out the non-contiguous case.
Hence, a $1$-component may contain different $2$-components, which may partially overlap (share some nodes), and the $2$-components may contain a certain number of $3$-components, and so on. The resulting is a hiearchy of node groups, which are more and more cohesive as we to deep into the hierarchy. Here is an example taken from the igraph manual.
# Create a graph with an interesting structure g = graph.disjoint.union(graph.full(4), graph.empty(2,directed=FALSE)) g = add.edges(g, c(4,5,5,6,5,3)) g = graph.disjoint.union(g,g,g) g = add.edges(g,c(1,7,2,8,1,13,5,1,5,2)) # Find cohesive blocks gBlocks = cohesive.blocks(g) # Examine block hierarchy, size and cohesion gBlocks # Print nodes of blocks blocks(gBlocks)
The number of node-independent paths between two nodes is also known as the connectivity of the two nodes. It can be thought as a measure of how strongly connected the two nodes are. The connectivity of a graph (also known as cohesion of a graph) is the minimum connectivity of all pairs of nodes in the graph. The smallest set of vertices that would have to be removed in order to disconnect two nodes not linked by an edge is called the minimum cut set for the two vertices. A corollary of Menger's theorem in graph theory claims that the size of the minimum cut set for two nodes not linked by an edge is exactly the connectivity of the two nodes. It follows that a $k$-component remains connected as soon as less than $k$ nodes (and the incident edges) are removed. For instance, a bicomponent is still connected if we remove any of its nodes.
For these reasons, the idea of $k$-component is associated with the idea of network robustness. In data networks such as Internet the connectivity of two routers is the number of independent routes that data might take between the two routers, and it is also the minimum number of routers that would have to fail to cut the data connection between the two endpoints. One would hope that most of the network backbone is a $k$-component with high $k$, so that it would be difficult for points on the backbone to lose connection with one another.
As for normal connected components, usually there is one large biconnected component, and many much smaller biconnected components. For example, we have analyzed the collaboration network for computer science. Two computer scientists are linked if they published at least one paper together, as recorded in DBLP, the most complete bibliography for computer science. The network contains 688,642 nodes and 2,283,764 edges. The computer science collaboration network is widely connected. The largest connected component counts 583,264 scholars, that is 85% of the entire network. There are two second largest components, the size of which, only 40 nodes, is negligible compared to that of the giant component. The largest biconnected component counts 418,001 nodes, or 61% of the entire network, and it covers a share of 72% of the largest connected component. The second-largest biconnected component has only 32 nodes.
The component structure of directed networks is more complicated than for undirected ones. Directed graphs have weakly and strongly connected components. Two vertices are in the same weakly connected component if they are connected by a path, where paths are allowed to go either way along any edge. The weakly connected components correspond closely to the concept of connected component in undirected graphs and the typical situation is similar: there is usually one large weakly connected component plus other small ones.
Two vertices are in the same strongly connected component if each can reach and is reachable from the other along a directed path. Strongly connected components form a partition of the vertex set and define an equivalence relation among nodes. Not all directed networks have a large strongly connected component. In particular, any acyclic network has no strongly connected components of size greater than one. Real-life networks that are (almost) acyclic are article citation networks and food webs.
The command cluster computes components for directed networks as well. It has a mode parameter which can have values weak or strong to compute weakly and strongly connected components. Here is an example of a directed network with the largest strongly connected component highlighted in red:
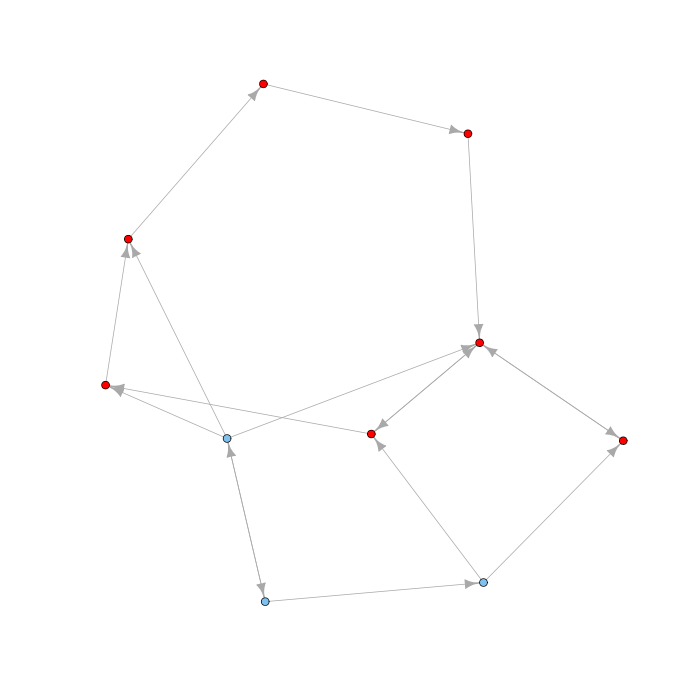
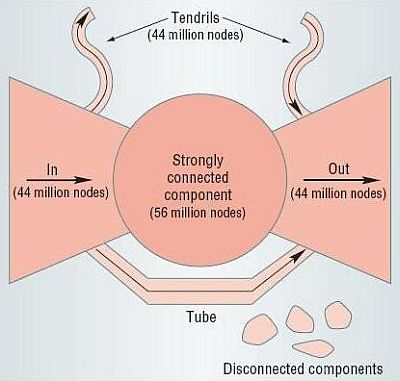
Associated with each strongly connected component is an out-component (the set of vertices that can be reached from the strongly connected component but that cannot reach it) and an in-component (the set of vertices that can reach the strongly connected component but that are note reachable from it). Note that in and out components are disjoint: if a node would belong to both the in and out component of a strongly connected component, then that node would be part of the strongly connected component. The overall picture for a directed network is that of a bow tie diagram, like that for the Web below: