Local clustering is sometimes used as a measure of centrality, as well as a way to study the large-scale structure of a network. Here we discuss clustering as a centrality measure. The clustering coefficient $C_i$ of a vertex $i$ is the frequency of pairs of neighbors of $i$ that are connected by an edge, that is, it is the ratio of the number $m_i$ of pairs of neighbors of $i$ that are connected and the number of possible pairs of neighbors of $i$, which is $k_i (k_i - 1) / 2$, where $k_i$ is the degree of $i$:
$\displaystyle{C_i = \frac{2 m_i}{k_i (k_i - 1)}}$
In other words, $C_i$ is the probability that a pair of neighbors of $i$ are connected. The values of $C_i$ ranges from 0 to 1: the lower bound represent the situation where no pairs of neighbors of $i$ are connected, while the upper bound holds when all pairs are linked. In the latter case, the set of neighbors of $i$ extended with $i$ itself forms a complete graph or clique, that is a graph where each pair of node is connected by an edge.
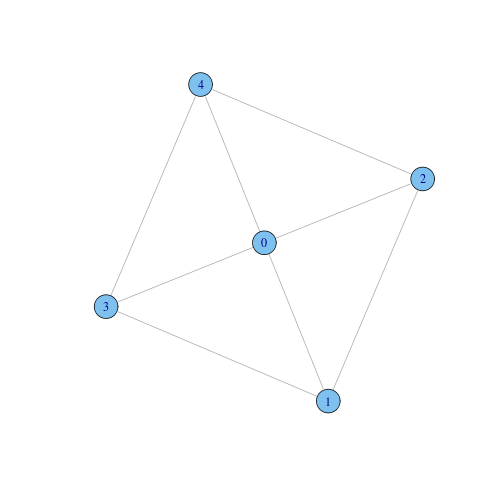
For example, consider the next undirected graph. Node 0 has 4 neighbors, and 4 pairs over 6 among these neighbors are linked. Hence $C_0 = 4/6 = 0.66$. Node 1 (as well as nodes 2, 3, and 4) has 3 neighbors, and 2 pairs over 3 among them are connected, hence $C_1 = 2/3 = 0.66$.

Function transitivity (R, C) computes local (and global) clustering.
Local clustering can be used for a probe for the existence of so-called structural holes in a network. While it is common, mainly in social networks, for the neighbors of a vertex to be connected among themselves, it happens sometimes that these expected connections are missing. The missing links are called structural holes. If we are interested in efficient spread of information or other traffic around a network, then structural holes are a bad thing, since they reduce the number of alternative routes information can take.
On the other hand, structural holes are a good thing for the central vertex $i$ whose friends lack connections, because they give $i$ power over information flow between those friends. If two friends of $i$ are connected directly then they can exchange information directly without bothering $i$. On the other hand, if they are not connected, then there is a good change that they exchange information through $i$. The inverse $1 / C_i$ of the local clustering coefficient $C_i$ can be thought as a centrality measure: it takes high values (that is $C_i$ is low) if there are many structural holes among the friends of $i$, and hence $i$ is influential in the circle of their friends, and takes low values (that is $C_i$ is hight) if there are few structural holes among the friends of $i$, and hence $i$ has low influence on their friends.
Local clustering is like a local version of betweenness: where betweenness centrality measures a vertex's control over information flowing between all pairs of nodes in its component, local clustering measures control over flows between just the immediate neighbors of a vertex.
Assuming that we can check the if two nodes are connected by an edge in constant time, computing the local clustering coefficient for a node $i$ costs $O(k_{i}^{2})$, where $k_i$ is the degree of $i$, since we have to check the existence of an edge for each pair of neighbors of $i$. Hence, computing the clustering coefficients for all nodes costs $\sum_i k_{i}^{2}$. This quantity depends on the degree distribution of the network. In the worst case, each $k_i = O(n)$, and hence the complexity is cubic $O(n^3)$. In the best case, each $k_i = O(1)$, and the complexity is linear $O(n)$. Real networks are sparse graphs, but contain hubs, nodes with a very high degree (notice that a hub with degree of the order of $n$ is sufficient to get a quadratic complexity). Hence, for real networks, we might expect the complexity to range between $O(n)$ and $O(n^2)$.